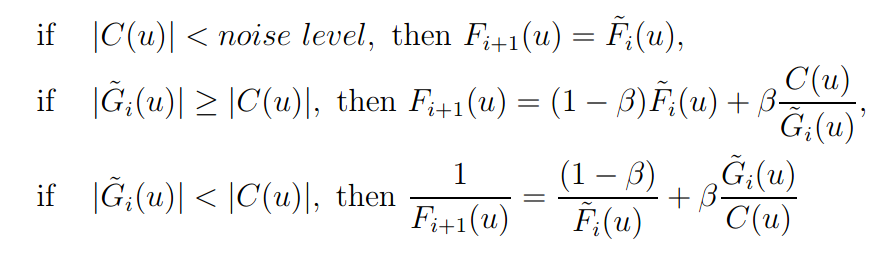This section discusses the development of approaches to the ill-posed problem of blind deconvolution. First general deconvolution techniques assuming a known psf are presented. Then approaches for blind deconvolution with standard imaging systems are presented, along with a few means of accelerating their typically lengthy execution times.
Single Channel Multi-frame Blind Deconvolution
In 1972, Gerchberg and Saxton (GS) presented an algorithm “for the rapid solution of the phase of the complete wave function whose intensity in the diffraction and imaging planes of an imaging system are known.” The algorithm iterates back and forth between the two planes via Fourier transforms. The problem is constrained by the degree of temporal and/or spatial coherency of the wave.
Additionally, the constraint of the magnitudes between the two planes results in a non-convex set in the image space according to Combettes. The algorithm is outlined in Figure 1.
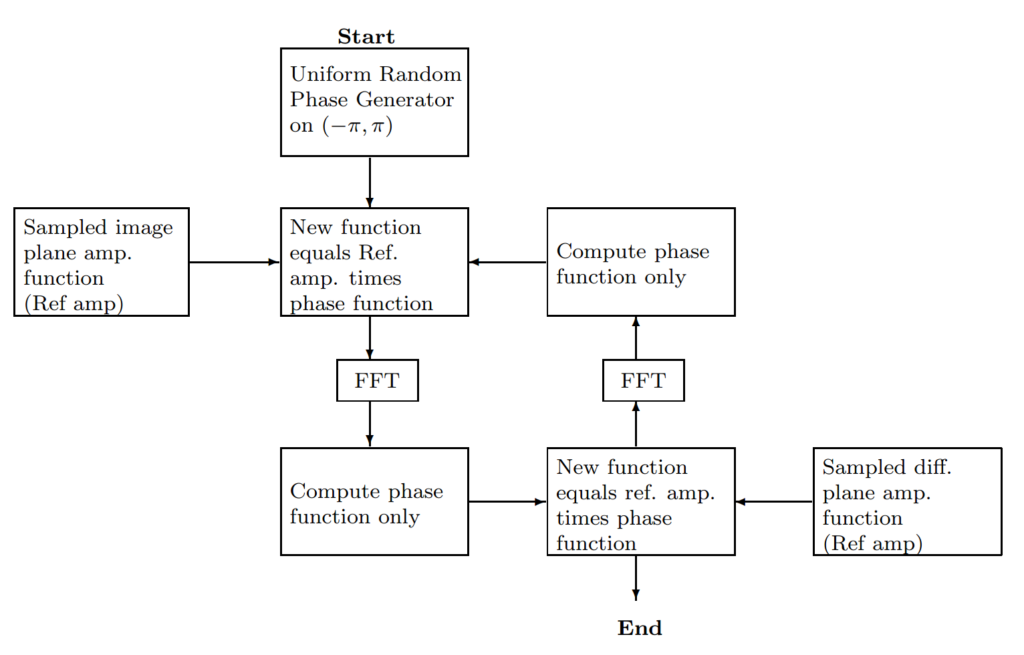
The inputs to the algorithm are the two input amplitude functions from the image and diffraction planes. A uniformly random phase generator is used to give the algorithm an initial starting point. GS offer a proof that the squared error between the results of the Fourier transforms and the input amplitude functions must decrease or remain the same on each iteration. They also point out that the solution reached is not unique.
Also, in 1972, Richardson introduced the use of Bayesian-based probability methods to restore noisy degraded images with a known psf. This was an improvement over the Fourier transform methods that performed well in a noiseless environment but degraded quickly with increased noise. The degraded image, H, is the convolution of the original image, W, with the point spread function, S, where all three are assumed to be discrete probability distribution functions. Two assumptions are made:
- S is normalized with respect to amplitude,
- The total energy in H is equivalent to the total energy in W.
An iterative algorithm is developed using Bayes’ Theorem. The initial estimate assumes a uniform distribution and results in the equation
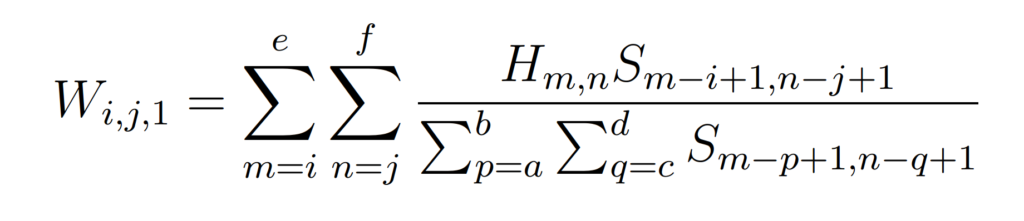
and subsequent iterations have the form
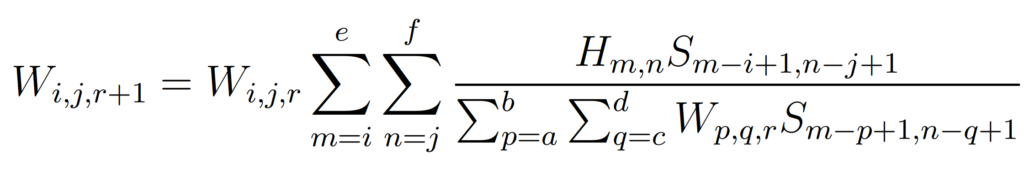
where
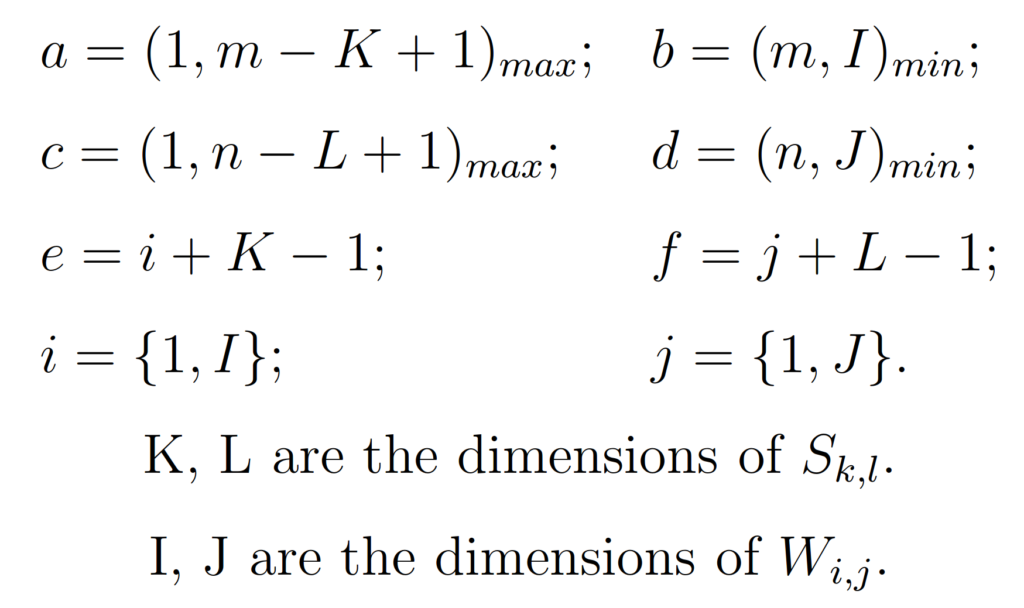
After the initial estimate, the W term on the right side of Richardson Equation 2 acts as a corrective factor to the convergence of the algorithm. The approach seems to keep S fixed throughout the execution of the algorithm. The algorithm demonstrated convergence in all cases tried by Richardson but no proof of convergence was developed.
In 1974, Lucy introduced another iterative technique based on increasing the likelihood of the observed sample each iteration. It is derived from Bayes’ Theorem and conserves the normalization and non-negativity constraints of astronomical images. The combination of both the Richardson algorithm and the Lucy algorithm is commonly referred to as the Richardson-Lucy (RL) algorithm.
In 1982, Fienup compares iterative phase retrieval algorithms to steepest-descent gradient search techniques along with other algorithms. He discusses convergence rates and details some error functions for the algorithms. The first algorithm discussed is the error-reduction algorithm which is a generalized GS algorithm. It is applicable to the recovery of phase from two intensity measurements, like the GS algorithm, as well as one intensity measurement with a known constraint. In the area of astronomy, the known constraint is the non-negativity of the source object.
The error-reduction algorithm consists of the following four steps:
- Fourier transform gk(x) producing Gk(u)
- Make minimum changes in Gk(u) which allow it to satisfy the Fourier domain constraints producing G’k(u)
- Inverse Fourier transform G’k(u) producing g’k(x)
- Make minimum changes to g’k which allow it to satisfy the object domain constraints yielding gk+1(x)
where gk(x) and G’k(u) are estimates of f(x) and F(u), respectively.
For problems in astronomy with a single intensity image, the first three steps are identical to the first three steps of the GS algorithm. The fourth step applies the non-negativity constraint such that
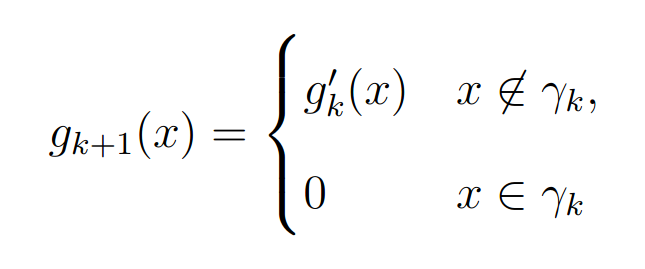
where γ is the set of points dependent on k, where g’k(x) violates the non-negativity constraint, i.e. where g’k(x) < 0.
For the case of a single intensity measurement with constraint, Fienup’s error measure is
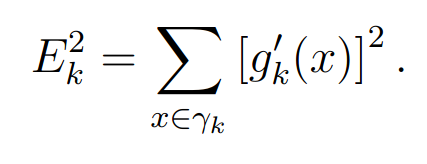
He found that the “error-reduction algorithm usually decreases the error rapidly for the first few iterations but much more slowly for later iterations.” He states that for the single image case convergence is “painfully slow” and unsatisfactory for that application.
According to Fienup, in 82, a method proven to converge faster for both cases is the input-output (IO) algorithm. The IO algorithm differs from the error-reduction algorithm only in the object domain. The first three operations are the same for both algorithms. If those three operations are grouped together as shown in Figure 2 they can be viewed as a nonlinear system having input g and output g’. “The input g(x) no longer must be thought of as the current best estimate of the object; instead it can be thought of as the driving function for the next output, g'(x).”
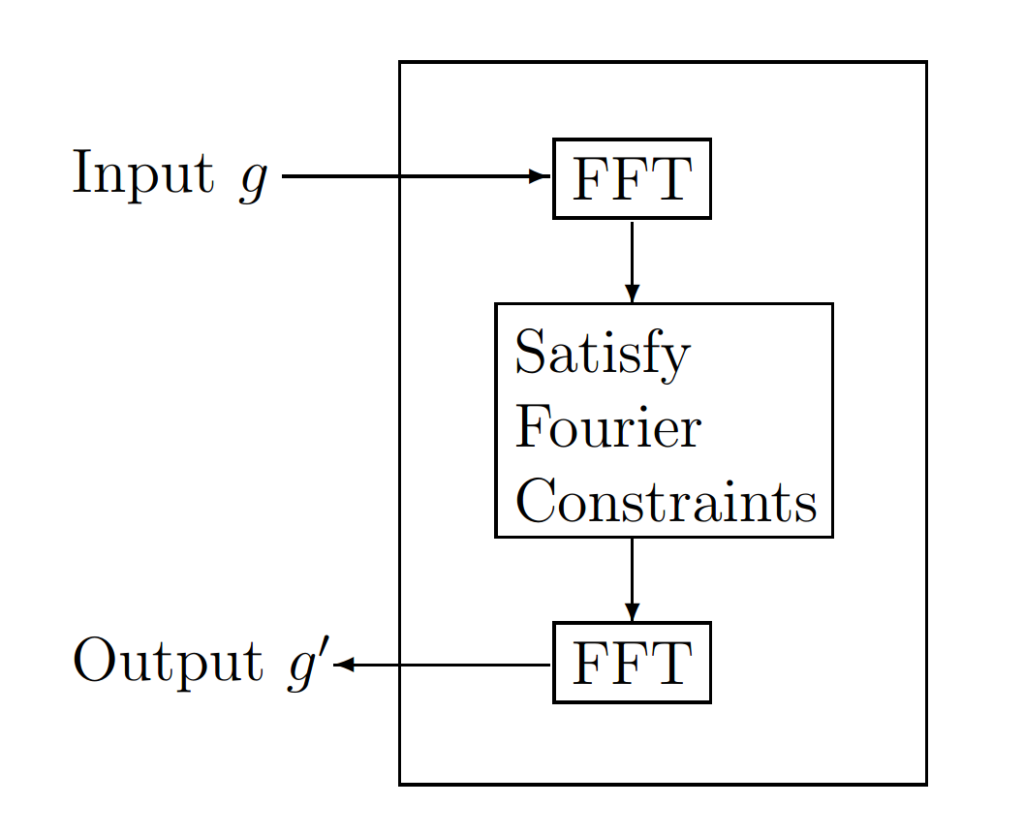
The basic IO algorithm uses the following step to get the next estimate
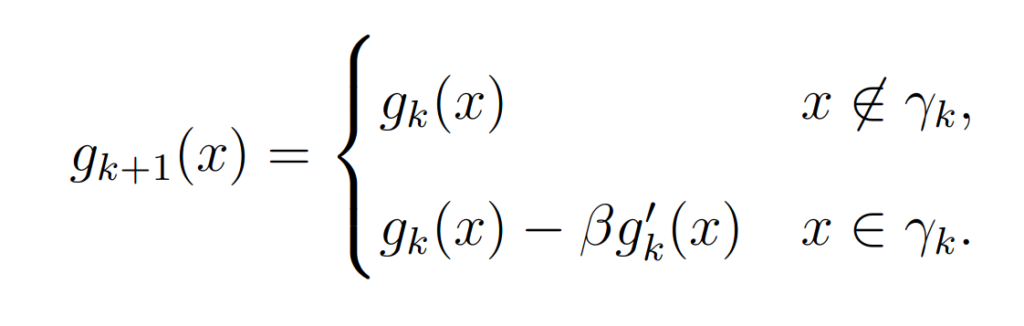
The output-output algorithm is a modified IO algorithm and uses the following step to get the next estimate
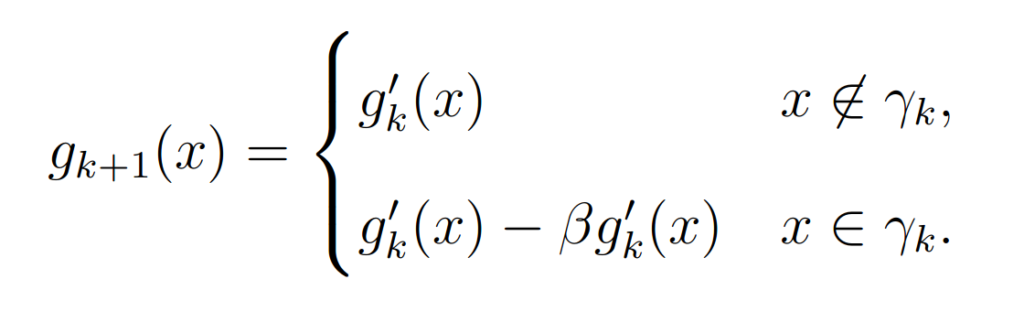
The hybrid IO algorithm uses the following step to get the next estimate
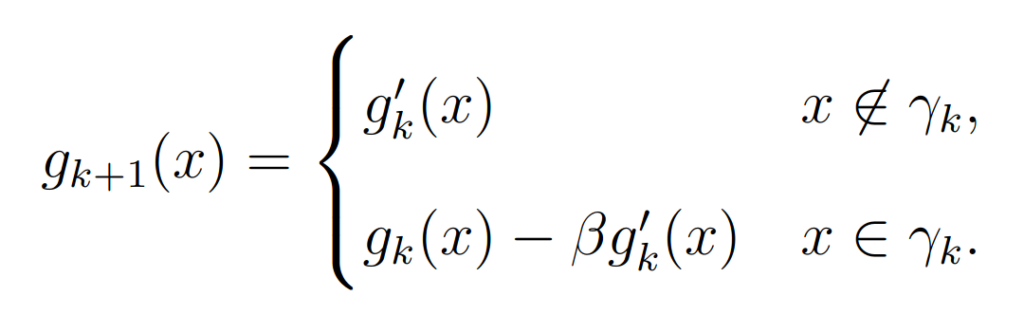
“The hybrid input-output algorithm is an attempt to avoid a stagnation problem that tends to occur with the output-output algorithm.” The output-output algorithm can stagnate with no means to get out of this state, but the hybrid input continues to grow until the output becomes non-negative.
Fienup analyzed the performance differences between the gradient search and the various IO algorithms for the case of phase retrieval from a single intensity image. Various values of β are used in the experiments. The optimal β value varied with the input and the algorithm. The hybrid seemed to have the best overall performance but was unstable and tends to move to a worse error before decreasing to a lower error than the other algorithms.
In 1988, Ayers and Dainty introduced another iterative method for the blind deconvolution of two convolved functions
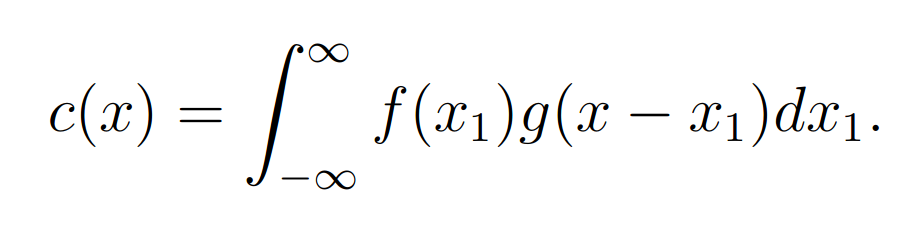
It is similar to the iterative error-reduction algorithm but requires a priori knowledge of both functions convolved to produce the single convolved image. A flow chart of the algorithm is shown in Figure 3.
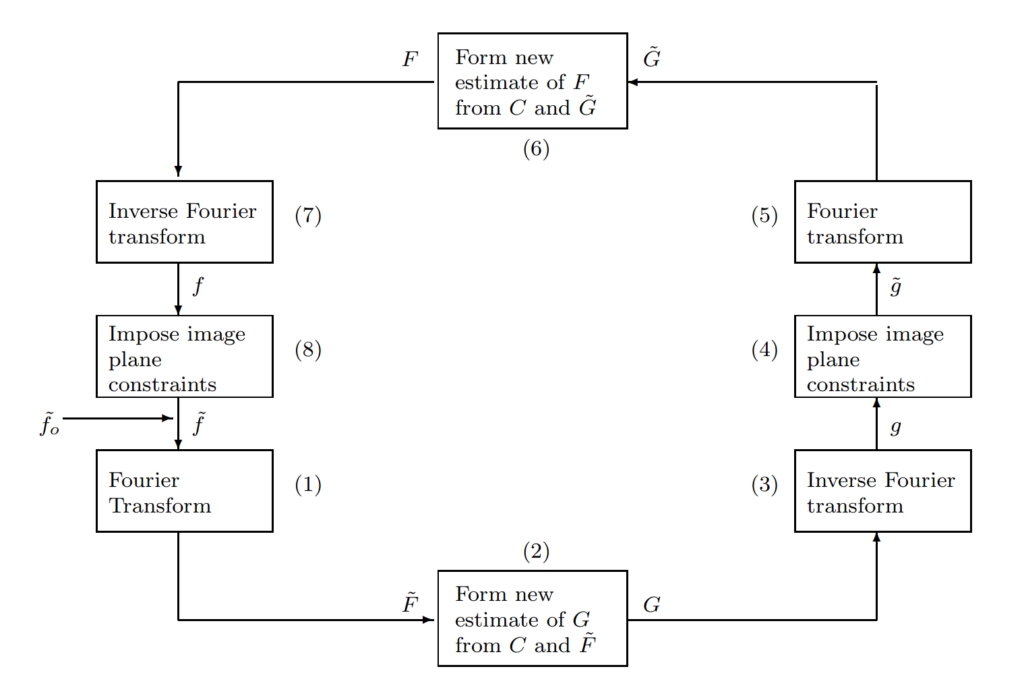
A priori information is required for this algorithm. The example given assumes non-negativity of both functions f(x) and g(x). A non-negative initial estimate \tilde{f}_o(x) is generated as the starting point. This is Fourier transformed to produce \tilde{F}(u) in Step 1. Then \tilde{F}(u) is inverted to form an inverse filter and multiplied by C(u) to produce an estimate G(u). Step 3 inverse Fourier transforms G(u) to produce g(x). The image constraints are imposed by setting all points in g(x) that are negative to zero yielding \tilde{g}(x). In Step 5 a Fourier transforms of \tilde{g}(x) produces \tilde{G}(u). Step 6 inverts \tilde{G}(u) to produce another inverse filter and multiplies by C(u) to yield the spectrum estimate F(u). Step 7 inverse Fourier transforms F(u) to produce the function estimate f(x) and the non-negativity constraint is applied to complete the loop.
Two major problems with this algorithm are:
- The inverse filters in Steps 2 and 6 are problematic due to inverting regions of low values.
- Zeros at particular spatial frequencies in either F(u) or G(u) result in voids at those frequencies in the convolution.
The non-negativity constraint is imposed similarly to previous algorithms with an additional energy conservation that seems to increase the rate of convergence and is defined as:
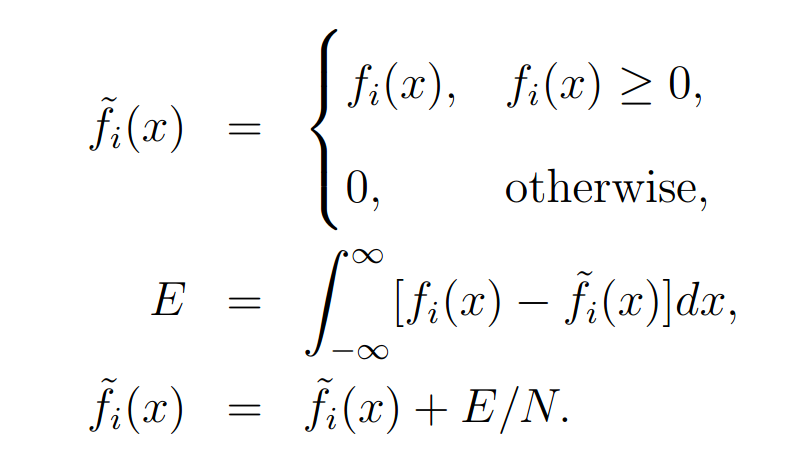
where N is the number of pixels in the image.
The Fourier domain constraint is more complicated, partly to mitigate the two significant problems pointed out previously, and are summarized as follows:
where $0 \leq \beta \leq 1$. On each iteration the two Fourier domain estimates are averaged. The averaging does not affect the convergence rate, however, the convergence rate is dependent on $\beta$, but no method of finding the optimal value of $\beta$ was found.
An additional method to address extended regions of low or zero values is introduced. A weighting function is introduced that is non-zero up to some band-limit. The one used by Ayers and Dainty is the one that naturally occurs with the incoherent transfer function of a circular aperture. After a new spectrum estimate is produced by the averaging process it is multiplied by the weighting function. Then, “after subsequent imposition of the image domain constraints the updated spectrum estimate is divided by the weight function.”
Ayers and Dainty stress “that the uniqueness and convergence properties of the deconvolution algorithm are uncertain and that the effect of various amounts of noise existing in the convolution data” is unknown.
In 1990, \emph{Seldin} and \emph{Fienup}\cite{seldin90} applied the Ayers and Dainty (\abbreviation[Ayers and Dainty]{AD}) algorithm to the specific case of phase retrieval. The algorithm is compared to the error-reduction and hybrid input-output algorithms previously discussed with various levels of additive Gaussian noise. Instead of implementing the Fourier domain constraint in Equation \ref{FDC} outlined by Ayers and Dainty, Seldin and Fienup use a Wiener-Helstrom filter instead. The end result is an algorithm that differs from the error-reduction algorithm only in the Fourier-domain constraint. The Fourier-domain constraint for the error-reduction algorithm is
F_k(u) = \tilde{F}_k(u) \frac{|F(u)|}{|\tilde{F}_k(u)|}
and the Fourier-domain constraint for the AD algorithm is
F_k(u) = \tilde{F}_k(u) \frac{|F(u)|^2}{|\tilde{F}_k(u)|^2}.
Seldin and Fienup show that the error-reduction algorithm and the AD algorithm are similar both in form and in performance. The error-reduction algorithm seemed to perform better at higher noise levels than the AD algorithm but the hybrid IO algorithm clearly outperformed both of them.
In 1992, Holmes introduced an iterative expectation-maximization (EM) approach to the blind deconvolution problem. Primary focus is on wide-field and confocal fluorescence microscopy. Holmes extends the maximum-likelihood (ML) estimation introduced by Shepp and Vardi to incoherent imaging. Two constraints are imposed on the algorithm: