Light has been contemplated and studied since the ancient Greeks. So what is light? Light is composed of finite quanta called photons. Each photon is a transverse electromagnetic wave in free space. What this means is that there is an electric component and a magnetic component that are perpendicular to each other and at the same time both are perpendicular to the direction of its propagation. A lot of information can be gained by analyzing the light coming from an object, whether the object is the source of the light or merely reflecting it. The light from a distant star provides a lot of information about it. A spectral analysis of the light can tell us what the star is made of, how big it is, how hot it is, etc. at the same time, light reflected from an object can provide information about it as well.
When considering the light coming from an object there are three properties, shown in Fig 1, that can be measured. The first is how much light is coming from the object. This quantity is called the intensity of the light and is determined by the number of photons collected. The intensity may change over time as angles in the imaging scenario change or as the object changes its articulation or rotation. The second measure of light coming from the object is the spectrum or frequency of the light. This is determined by a combination of the source light and the material that is reflecting it. Both of these properties of light have been exploited significantly in the development of solutions to the non-resolved space object identification (SOI) inverse problem. “This inversion problem is mathematically ill-posed; i.e. small errors in the data may have large effects on the results. Also, the number and range of the observing geometries have a significant effect on the inversion.[Kaas92]” Given these impacts of small errors on the inversion problem all information available from the light coming from an object should be used.
Figure 1 here.
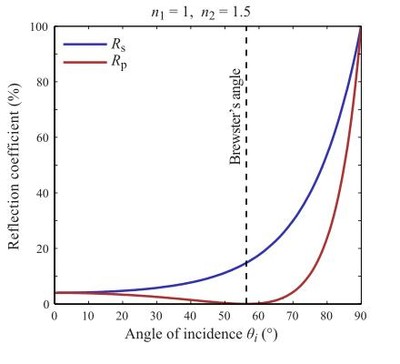
Initial efforts focused on the intensity of the photometric light curves produced by the object under observation. More recently, the frequency of the light has been considered in the identification, classification, and material analysis of objects resulting in better constrained solutions. All light has a third property that can be collected and used to further constrain the solution space. This is the polarization of the light or in other words the orientation of the photons coming from the object. This polarization is effectively additional embedded information that can be exploited. The polarization of the light from an object is governed by its interaction with the surface that reflects it. The shape, material, surface properties, and incidence angles, see Fig 2, all have an affect on the reflected light. Thus the reflected light contains embedded information on the object itself if it can be successfully extracted and will better constrain the characterization of space objects. The level of information extracted is directly related to the level of representation of the polarization information captured.
The polarization can be represented and measured with different levels of fidelity, including: Jones vectors and associated calculus, Meuller matrices, coherency matrices, Stokes vectors, Poincare spheres, or Stokes space. Jones vectors are limited in scope and do not handle changing polarization states. Meuller matrices were designed to handle depolarizing effects but are still somewhat lacking in the ability to handle the stochastic nature of this problem domain. Stokes vectors are much better able to handle stochastic processes that occur in the imaging domain. In 2D space, the Stokes vectors can be placed in a geometric interpretation called a Poincare sphere. Different places on the sphere correspond to the different types of polarizations, i.e. linearly polarized, circularly polarized, etc. However, difficulties exists when trying to represent all four degrees of freedom in S when considering partially polarized light. A better representation is to use a Hilbert space S with coordinate axes S0, S1, S2, S3. This is a complete Stokes space where the Stokes vectors must satisfy the inequality S0^2 >= S1^2 + S2^2 + S3^2 [Foreman10].
Information theory can be used to characterize the effects polarization has on the photometric light curve inversion problem domain. The most likely models used or developed will be multi-parameter unbiased Bayesian estimators. This allows the use of the Cramer-Rao inequality to be used for calculation of the lower bound on the variance of any unbiased estimate [VanTrees]. The imaging models for the polarization effects will most likely incorporate the use of Meuller matrices at least or for better representation of polarization Stokes vectors will be used.
One of the uses of the resulting polarization information is the detection of surface normals. “Taking polarization images from multiple views produces enough constraints to infer the complete surface shape [Rahmann01].” Even when the object is not resolvable the information is still encoded in the reflected light. For greater accuracy and because of the sensitivity of polarization to the angle of the incident light, observations should be gathered over an extended period of time. This allows for the variation across the solar cycle to be captured and its effects to be quantified.
This research considers the mostly overlooked third characteristic of light and its impact on space situational awareness. This is an extension of more than 30 years of research aimed at getting more information from photometric light curves. The problem domain is ill-posed and any additional information better constrains the problem resulting in better solutions. Whereas past efforts have primarily looked at intensity, and more recent research has added spectral content, the use of polarization information should add significant constraints to the problem space. This leads to more accurate and/or faster characterization and identification of non-resolved space objects. This increases the ability of current and future optical systems to track, characterize, and identify space objects.